2359 . EZDSA
TopCoder
Tags
Description
//r: 027a872f87c98bf7aead3c514ffb9e5f25719c7d5d4591aa34f3e3388110807d
//s: 4ed20d3dc3265e845fd13c021ca8dce97f2361565e030e5b05d2ccf58dc5357f
//x: 04df4bd35d60b090d6a9da5360479e08fc6fc2b6ece2d5f989735836bb0e508a
//y: 7349916cdf36d4830f752a47ac7ff518bfa8ac92cbad4ad66e9f06e7943deedf
以上是本題的橢圓曲線數位簽章,可以用來證明本題的確是出題者出的(雖然這是廢話)。
什麼?你說你不知道橢圓曲線數位簽章是什麼?
ECDSA (Elliptic Curve Digital Signature Algorithm) 是一種基於橢圓曲線密碼學的數位簽章算法。
在了解什麼是 ECDSA 前,我們要先來簡單了解一下橢圓曲線是怎麼運作的。
模下橢圓曲線 Modular Elliptic Curve
在密碼學中,我們在意的是在模某個質數 $p$ 下的橢圓曲線。
給定一個質數 $p$ 和兩個整數 $a, b \in \mathbb{Z}_p$,我們可以定義出一個橢圓曲線 $\Gamma: y ^ 2 \equiv x ^ 3 + ax + b \pmod{p}$。
我們說一個點 $(x, y)$ 在 $\Gamma$ 上若他符合上式。
此外,我們特別定義一個無限遠的點 $O$ 也在此模下橢圓曲線上。
對於 $\Gamma$ 上兩相異點 $P, Q$,我們令他們相加的點 $R$ 為過 $P, Q$ 的直線交於 $\Gamma$ 的第三點對 $X$ 軸對稱的那個點。
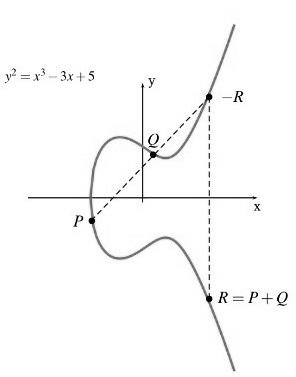
第三點 $R = (x_R, y_R)$ 可以由 $s = \frac{y_Q - y_P}{x_Q - x_P}, x_R = s ^ 2 - x_Q - x_P, y_R = s(x_P - x_Q) - y_P$ 算出。
如果 $P$ 或 $Q$ 是切點,那 $R$ 就是切點對 $X$ 軸的對稱點。可以證明上式依然成立。
如果是 $P + P$ 的話,我們定義 $R$ 是過 $P$ 的切線交於 $\Gamma$ 的第二點對 $X$ 軸對稱的那個點。
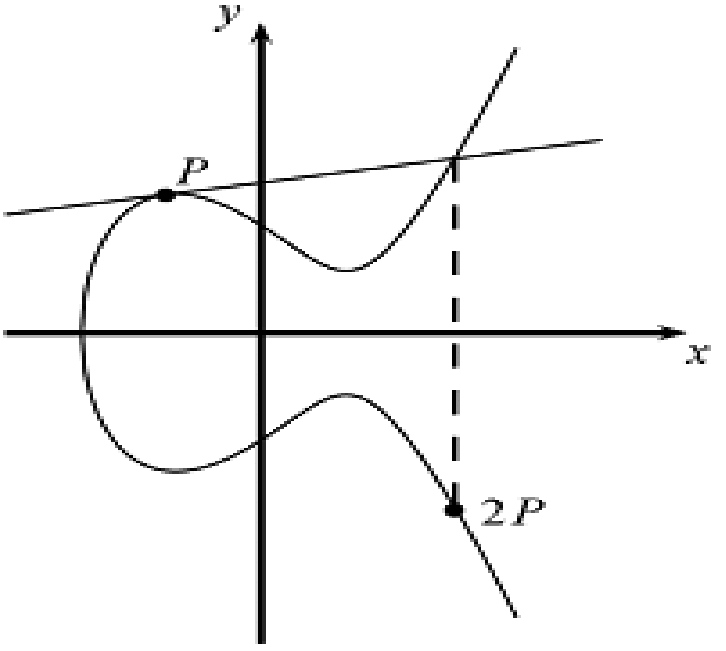
此時以 $s = \frac{3x_P ^ 2 + a}{2 y_P}$ 代入上式即可得到 $R$。
可以證明 $\Gamma$ 上的所有點(包含無限遠點 $O$)和上述的加法會形成一個交換群。
橢圓曲線離散對數問題 Elliptic Curve Discrete Log Problem (ECDLP)
給定一兩的點 $P, Q$ ,求出一個整數 $d$ 使得 $P + P + \ldots + P = dP = Q$ 。
這類問題通常很難在合理的時間內解出,除非有特殊的性質($d$ 太小、$\Gamma$ 的階太平滑或洽好是 $p$ 等)可以被攻擊。
這也是橢圓曲線數位簽章(ECDSA)的基礎。
橢圓曲線數位簽章算法 Elliptic Curve Digital Signature Algorithm (ECDSA)
數位簽章是一種使用了公鑰密碼學的技術。數位簽章就如同紙本簽章一樣,能被用來確認訊息發送者的身份是否正確,同時使發送者無法否認。
而 ECDSA 則是透過了 ECDLP 的難度來達到難以偽造及難以否認的特點。
更準確來說,ECDSA 需要滿足「正確性」(被正確簽署的簽章總是要被驗證為正確的)和「難以偽造」(沒辦法在合理時間內偽造)兩個性質。
具體來說,假設愛麗絲要用他的私鑰 $d$(一個正整數)簽署一個訊息 $M$(可以視為一個字串)而鮑伯想要驗證,
那麼最常見的實作方式是他們先決定好:
- 一個橢圓曲線 $\Gamma$,
- $\Gamma$ 上一個點 $G$,
- 算好 $G$ 在 $\Gamma$ 上的階 $n$,
- 愛麗絲的公鑰 $Q = dG$,以及
- 一個雜湊函數 $H$。
以上的資訊皆可以被公布,不會影響到簽章的安全性及完整性。
接下來,給定一個訊息 $M$ ,愛麗絲就可以用以下的步驟簽署 $M$:
- 隨機地抽一個 $[1, n - 1]$ 之間的神祕隨機數 $k$,並保持祕密。
- 令點 $P(x, y) = kG, r = x \bmod{n}$,計算 $s = k ^ {-1} (H(M) + rd) \bmod{n}$。
- 如果 $r = 0$ 或 $s = 0$ ,則重新挑一個 $k$ 。否則,告訴鮑伯 $M, r, s$ 。
特別注意,若 $k, d$ 被其他人得知其中一者,則此人便可以偽造愛麗絲的簽章(方法留給讀者當練習)。
而鮑伯可以由以下步驟驗證簽章 $M, r, s$:
- 檢查 $Q$ 的確是 $\Gamma$ 上的點,且 $nQ$ 確實是 $(\Gamma, +)$ 上的單位元 $O$。
- 令 $u_1 = H(m) s ^ {-1} \bmod{n}, u_2 = r s ^ {-1} \bmod{n}$,計算 $P'(x', y') = u_1 G + u_2 Q$。
- 檢查 $x'$ 是否為 $r$。如果否,則此簽章無效。如果是,則賭此簽章有效。
可以注意到簽章通過檢驗並不百分之百保證是愛麗絲簽的,因為就算 $k, d$ 並未被洩漏,其正確性仍基於:
- $H$ 沒有碰撞,
- 私鑰 $d$ 及所選的橢圓曲線 $\Gamma$ 是安全的,以及
- 攻擊者沒有花八百輩子的陽壽猜到 $k$ 或 $d$。
在本題實作中,我們考慮以 SHA256 作為 $H$ 而以 secp256k1 這個橢圓曲線做為 $\Gamma$ 的橢圓曲線數位簽章算法,且以簽章的正確性為唯一的考量。
現在,請你實作驗證簽章的演算法,也就是給你 $M, r, s, Q$ ,請你判斷這是不是一個正確的簽章。
實作細節
secp256k1 的參數如下:(來源:https://en.bitcoin.it/wiki/Secp256k1 )
- $p = $
0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEFFFFFC2F$= 2 ^ {256} - 2 ^ {32} - 2 ^ 9 - 2 ^ 8 - 2 ^ 7 - 2 ^ 6 - 2 ^ 4 - 1$ - $a = 0, b = 7$
- $G = (x, y) = ($
0x79BE667EF9DCBBAC55A06295CE870B07029BFCDB2DCE28D959F2815B16F81798$, $0x483ADA7726A3C4655DA4FBFC0E1108A8FD17B448A68554199C47D08FFB10D4B8$) = ($55066263022277343669578718895168534326250603453777594175500187360389116729240$, $32670510020758816978083085130507043184471273380659243275938904335757337482424$)$ - $n = $
0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141$ = $115792089237316195423570985008687907852837564279074904382605163141518161494337
TIOJ 上的 python 有 SHA256 可以使用。
Input Format
每筆測資有五行輸入。
第一行會輸入以十六進位表示的 $M$。
第二行會輸入以十六進位表示的 $r$。
第三行會輸入以十六進位表示的 $s$。
第四行會輸入以十六進位表示的 $Q$ 的 $x$。
第五行會輸入以十六進位表示的 $Q$ 的 $y$。
Output Format
如果你判斷簽章是正確的,請輸出 True,否則請輸出 False。
Sample Input 1
d41c263f9e2353fa78fb838a299aee2d1258392d37016230ca8b2154701461f7
bff555b3b919657d3fdedf784f475a551d6f5034de33715b1c43f462a01e6fb4
8ca0f0f5b5c378a20b7c670d754173d1a985ef3495aba4eaf1003c0a46c8c2f2
75771ac5ba51b8fcd810120de8e9131c7a0472d0c2d99ac0b98f762f412f5232
Sample Output 1
Sample Input 2
d41c263f9e2353fa78fb838a299aee2d1258392d37016230ca8b2154701461f7
bff555b3b919657d3fdedf784f475a551d6f5034de33715b1c43f462a01e6fb4
8ca0f0f5b5c378a20b7c670d754173d1a985ef3495aba4eaf1003c0a46c8c2f2
75771ac5ba51b8fcd810120de8e9131c7a0472d0c2d99ac0b98f762f412f5232
Sample Output 2
Hints
- 為什麼是愛麗絲和鮑伯?就只是翻成中文夠奇怪而已。
- 小知識:神祕隨機數的英文 Nonce 同時還有戀同癖、猥褻兒童罪犯的意思。英文真是神祕又隨機啊。
- 目前好像還沒有 Nonce 的公認翻譯,有的話拜託告訴出題者。
Problem Source
TIOJ April Fools Day Contest 2024 pI
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~1 | 範例測試資料。 | 0 |
| 2 | 0~3 | 無額外限制。 | 99 |
| 3 | 0~7 | 有額外限制。 | 1 |
