2195 . C. 粉刷護欄
TopCoder
Tags
Description
紅心國的黑桃國王為了促進國民身心健康,大力在國內修繕河濱自行車道,然而河道並不筆直,騎車時在彎道處不減速很容易衝出車道導致事故。為了減少事故,黑桃國王決定在彎道處搭建護欄,並找了方塊設計公司與梅花人力公司來完成這項工程。
護欄由多片長條形的木板並排而成(如下圖一)。方塊設計公司將設計圖交給了梅花人力公司,並且要求梅花人力公司將木板標記兩兩相異的編號。不巧的是,梅花人力公司的工人們把藝術大學護欄的設計圖和車道護欄的設計圖搞混了,藝術大學護欄如下圖二。已知藝術大學護欄滿足:
- 上下有 $2$ 條水平的木樑,所有木板均釘在這兩條木樑上。
- 每條木樑上等距離分成 $n$ 個點,其中上面木樑第 $i$ 個點釘著編號 $a_i$ 的木板,下面木樑第 $i$ 個點釘著編號 $b_i$ 的木板。
- 每根木板只會恰好釘在一個上木樑以及一個下木樑的點上。並且 $n$ 根木板釘的點都互相相異。
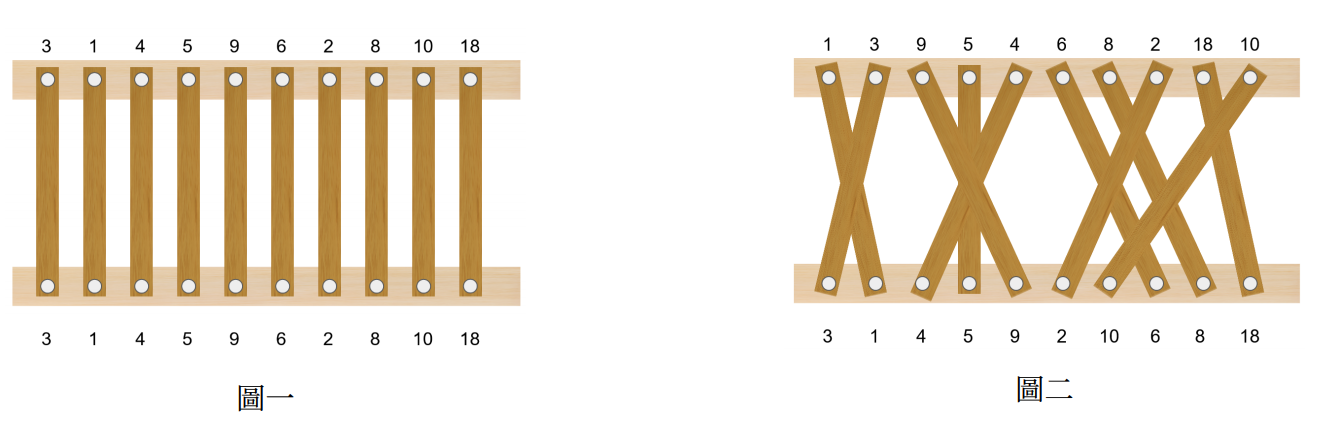
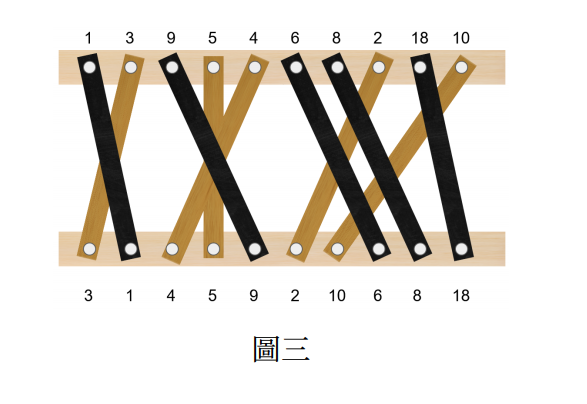
可想而知,這樣的成品是無法通過驗收的。方塊設計公司想了一個補救的辦法:從目前搭建好的護欄中,找出若干個從側面看上去兩兩不相交的木板,並將選出的木板漆上深的顏色。如此一來,視覺上也達到了和原設計護欄類似的效果。
方塊設計公司希望兩兩不相交的木板愈多愈好,請你寫一支程式來找出需要上漆的木板。以圖二為例,可選出 $5$ 片木板上漆,一個可能的上漆方式如圖三。
Input Format
$n$
$a_1\ a_2\ \dots\ a_n$
$b_1\ b_2\ \dots\ b_n$
- $n$ 為一整數代表每條木梁上點的數量。
- $a_i$ 為一整數代表上面木梁第 $i$ 個點釘著的木板編號。
- $b_i$ 為一整數代表下面木梁第 $i$ 個點釘著的木板編號。
Output Format
$c_1\ c_2\ \dots\ c_k$
- $k$ 為一整數代表從側面看上去兩兩不相交的木板的最大數量。
- $c_i$ 為一整數代表由左到右第 $i$ 個需要上漆的木板編號。
- 若有多個可上漆的方式,則輸出 $c_1c_2\dots c_k$ 字典序最大的。字典序是先按照 $c_1$ 以升序排列,如果 $c_1$ 一樣,那麼比較 $c_2$、$c_3$ 乃至 $c_k$。
Sample Input 1
1 3 9 5 4 6 8 2 18 10
3 1 4 5 9 2 10 6 8 18
Sample Output 1
Hints
測資限制
- $1\leq n \leq 2\times 10^ 5$。
- $a_1, a_2, \dots, a_n$ 為 $n$ 個相異非負整數。
- $b_1, b_2, \dots, b_n$ 和 $a_1, a_2, \dots, a_n$ 為同一群數字,僅順序不同。
- $0\leq a_i,b_i\leq 10^ 9$。($i\in\{1,2,\dots,n\}$)
- 上述所有變數均為整數。
評分說明
本題共有三組子任務,條件限制如下所示。每一子任務可有一或多筆測試資料,該組所有測試資料皆需答對才會獲得該組分數。
- (22%) $n\leq 10, \{a_1,a_2,\dots,a_n\}=\{b_1,b_2,\dots,b_n\}=\{0,1,2\dots,n-1\}$
- (33%) $n\leq 100$
- (45%) 無額外限制。
範例解釋
範例 1 說明:此範例對應圖二。最多可上漆的木板數量為 $5$,可能的上漆方式有 $(1, 4, 6, 8, 18)$,$(1, 5, 6, 8, 18)$,$(1, 9, 6, 8, 18)$,$(3, 4, 6, 8, 18)$,$(3, 5, 6, 8, 18)$,$(3, 9, 6, 8, 18)$ 六種,字典序最大者為 $(3, 9, 6, 8, 18)$。
Problem Source
2021 TOI 入營考 pC
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~9 | $n\leq 10, \{a_1,a_2,\dots,a_n\}=\{b_1,b_2,\dots,b_n\}=\{0,1,2\dots,n-1\}$ | 22 |
| 2 | 0~19 | $n\leq 100$ | 33 |
| 3 | 0~39 | 無額外限制 | 45 |
