2182 . 幸運表格 (Lucky)

Submit
Status
Discussion / Solution
Ranklist
Back to Problems List

TopCoder

腦子裝咖哩
想像不出自己 AC 的題目是實作不出來的！雖然想像得出來也不一定可以就是了

User's AC Ratio

96.9% (93/96)

Submission's AC Ratio

46.1% (123/267)

Tags

北市賽 2018-北市賽

Description

幸運表格是一種古老的遊戲，在 m×n 的表格中，每一個格子都被預先填入一個整數；接著玩家需要在蒙眼的狀況下選定一個格子做為他的起始位置，之後這位玩家只能在表格中「向右」或者「向下」移動，並且加上所有經過的格子上的整數數值，直到玩家的移動超出這個 m×n 的表格；此時，玩家所經過的所有數值的總和即為他的「幸運數」。您的任務是，給定一個 m×n 的表格，找出所有可能的幸運數中的最大值。

例如：在右圖一個 5×5 的表格中，每個格子分別被填入一個整數值接著，玩家從第二列第三欄的格子開始，依序往「下」「下」「右」「下」「下」移動，接著離開這個表格，則他的幸運數即為 8 –6+7 –3+4=10。然而，在這個例子中，若要達到最大可能的幸運數，則玩家需要從第三列的第一欄起始，接著往「右」「下」「右」「右」「下」「下」移動，其所達到的幸運數為 15。

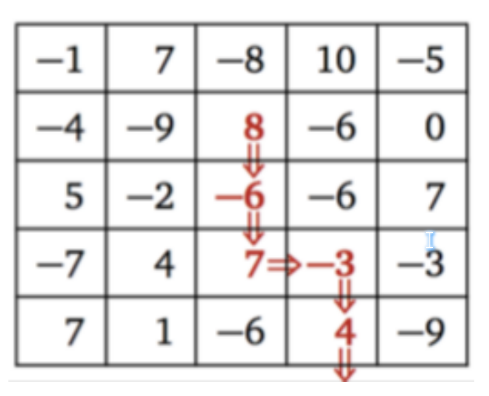
Input Format

輸入的第一行有二個以一個空白符號隔開的正整數 m 和 n，代表表格的列數和行數。接著 m 行中，每一行有 n 個空白符號隔開的整數，其中第 i 行的第 j 個整數，即代表表格中第 i 列第 j 欄的格子上的數字。每一個格子中的整數，必定大於 −100 且小於 100。

Output Format

請根據輸入的資料，輸出該個幸運表格所可能產出的最大幸運數。

Sample Input 1

2 2
5 -2
-3 1

Sample Output 1

4

Sample Input 2

5 5
-1 7 -8 10 -5
-4 -9 8 -6 0
5 -2 -6 -6 7
-7 4 7 -3 -3
7 1 -6 4 -9

Sample Output 2

15

Hints

本題共有四組測試資料，每組可有多筆測試資料：
第一組測試資料 m=n=2，共 15 分。
第二組測試資料 2<m=n≤5，共 20 分。
第三組測試資料 5<m=n≤100，共 28 分。
第四組測試資料 5<m≤1000,5<n≤1000，共 37 分。

Problem Source

107北市賽
testdata set by Omelet
註： 這裡的測資裡面最小的數字可以到 -1000，因為暫時應該不需要 rejudge 所以在這邊聲明就好。

Subtasks

No. Testdata Range Constraints Score
1 0~4 m=n=2 15
2 5~19 2<m=n≤5 20
3 20~29 5<m=n≤100 28
4 20~39 5<m,n≤1000 37

Testdata and Limits

No. Time Limit (ms) Memory Limit (VSS, KiB) Output Limit (KiB) Subtasks
0 1000 524288 65536 1
1 1000 524288 65536 1
2 1000 524288 65536 1
3 1000 524288 65536 1
4 1000 524288 65536 1
5 1000 524288 65536 2
6 1000 524288 65536 2
7 1000 524288 65536 2
8 1000 524288 65536 2
9 1000 524288 65536 2
10 1000 524288 65536 2
11 1000 524288 65536 2
12 1000 524288 65536 2
13 1000 524288 65536 2
14 1000 524288 65536 2
15 1000 524288 65536 2
16 1000 524288 65536 2
17 1000 524288 65536 2
18 1000 524288 65536 2
19 1000 524288 65536 2
20 1000 524288 65536 3 4
21 1000 524288 65536 3 4
22 1000 524288 65536 3 4
23 1000 524288 65536 3 4
24 1000 524288 65536 3 4
25 1000 524288 65536 3 4
26 1000 524288 65536 3 4
27 1000 524288 65536 3 4
28 1000 524288 65536 3 4
29 1000 524288 65536 3 4
30 1000 524288 65536 4
31 1000 524288 65536 4
32 1000 524288 65536 4
33 1000 524288 65536 4
34 1000 524288 65536 4
35 1000 524288 65536 4
36 1000 524288 65536 4
37 1000 524288 65536 4
38 1000 524288 65536 4
39 1000 524288 65536 4
Submit
Back to Top