2158 . 搶拉麵
TopCoder
Description
在競賽圈有個潛規則,你如果想要變強,你就要去吃碗拉麵,而且你吃的拉麵越好吃,你就會變得越強。
在天龍國裡,共有
其中
有
每個人都想吃最好吃的拉麵,
可是如果每個人都擠在同一間拉麵店的話,就要等很久。
聰明的你想到了一個辦法。
你規定所有人都只能前往和它距離
其中兩個座標
在這樣的狀況下,所有人都會前往他可以去的拉麵店中,做出最美味拉麵的店。
這樣一來,就不會所有人都擠在同一間拉麵店裡了
現在,你想知道,在精確的限制下,最多能有幾間拉麵店有人光顧
Input Format
第一行
接下來
接下來
Output Format
請輸出一個整數代表答案
Sample Input 1
3 3 1 1 1 2 1 2 2 3 3 0 1 1 3 3 3
Sample Output 1
2
Hints
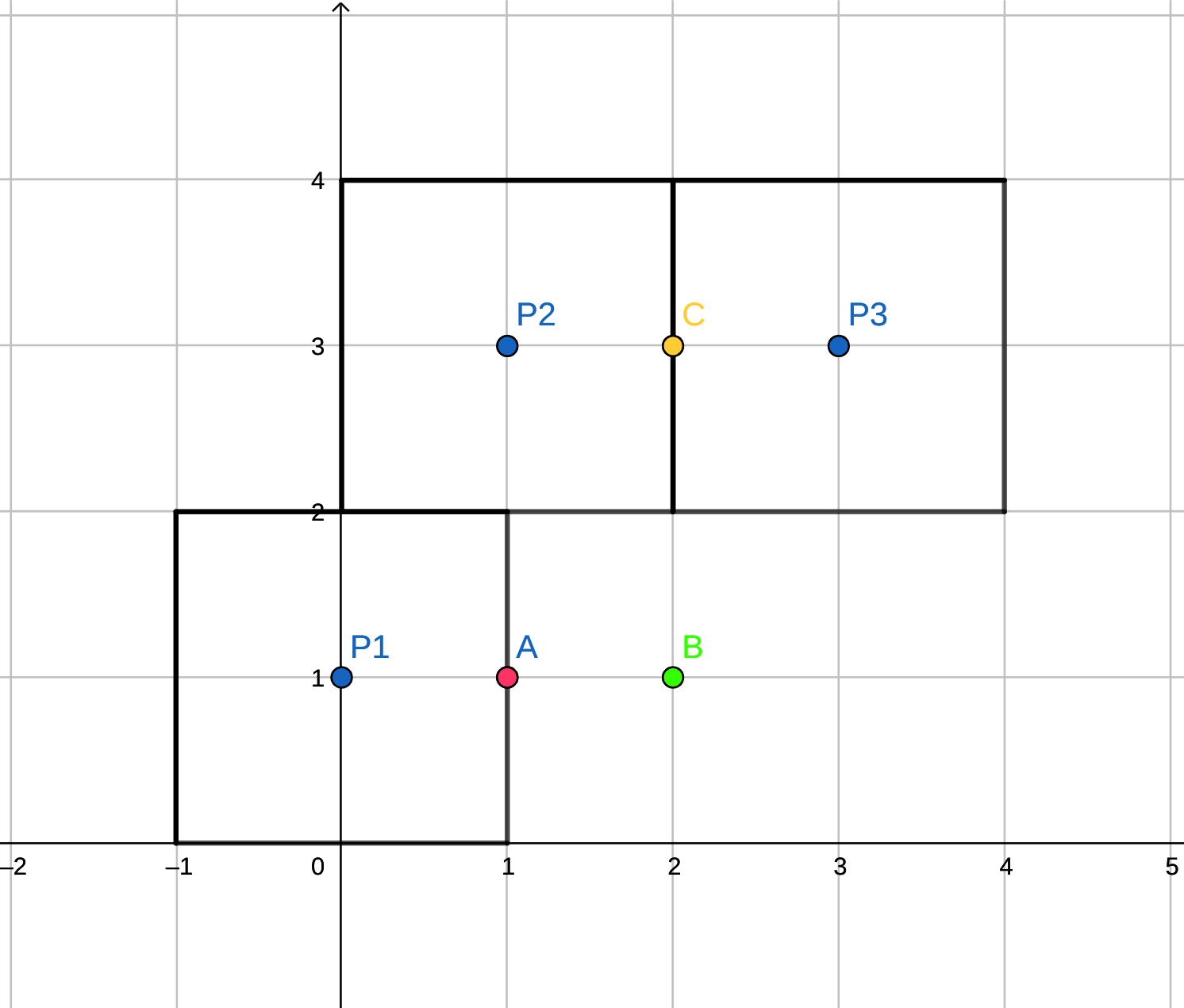
關於範測一
當我們將
編號為 1 的人將去 A (評價為 1) 的餐廳
而編號為 2, 3 都會去 C ( 評價為 3) 的餐廳
所以總共有兩間餐廳有人光顧
而且沒有其他的
Problem Source
by kevin_zhang
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~4 | 8 | |
| 2 | 5~9 | 8 | |
| 3 | 10~14 | 20 | |
| 4 | 15~19 | 24 | |
| 5 | 0~34 | No additional limits | 40 |
