1306 已加強測資並 rejudge
2038 . 馬拉松
TopCoder
Description
金氏運動公司打算舉辦一場馬拉松比賽,為了締造亮眼的完成比賽時間,金氏運動公司打算選擇性地邀請選手參賽。分析過往的數據資料,金氏運動公司觀察到以下二個現象:
(a) 對於任何一位選手,如果愈多他的朋友參賽,則他就能跑得愈快,所以傾向於找一群選手使得彼此互相認識的情況很多。因為認識是雙向的,如果
(b) 如果參賽的選手當中,存在兩位選手
現在金氏運動公司手上有一份
其中
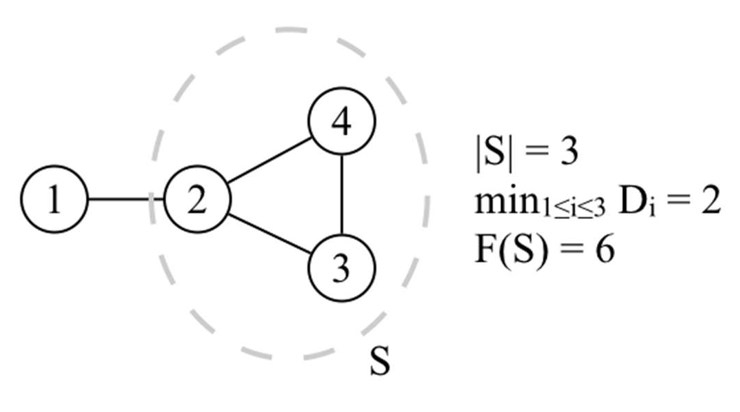
Input Format
每一組測試資料有兩列, 其中第一列有兩個正整數
Output Format
對於每組測試資料,輸出最大的
Sample Input 1
4 5 1 2 2 3 3 4 4 1 2 4
Sample Output 1
8
Sample Input 2
4 4 1 2 2 3 3 4 2 4
Sample Output 2
6
Sample Input 3
6 6 1 3 1 2 2 3 4 5 5 6 4 6
Sample Output 3
6
Hints
本題共有三個子題,每一子題可有多筆測試資料:
第一子題的測試資料中
第二子題的測試資料中
第三子題的測試資料中
Problem Source
106學年度高級中學資訊學科能力競賽決賽 程式設計試題第五題
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0~9 | 19 |
| 2 | 10~19 | 38 |
| 3 | 20~29 | 43 |
