2037 . 警力配置
Description
某警察局將負責巡邏 A 城市的
為了有效管理及節省開銷,局長希望從
範例說明:假設
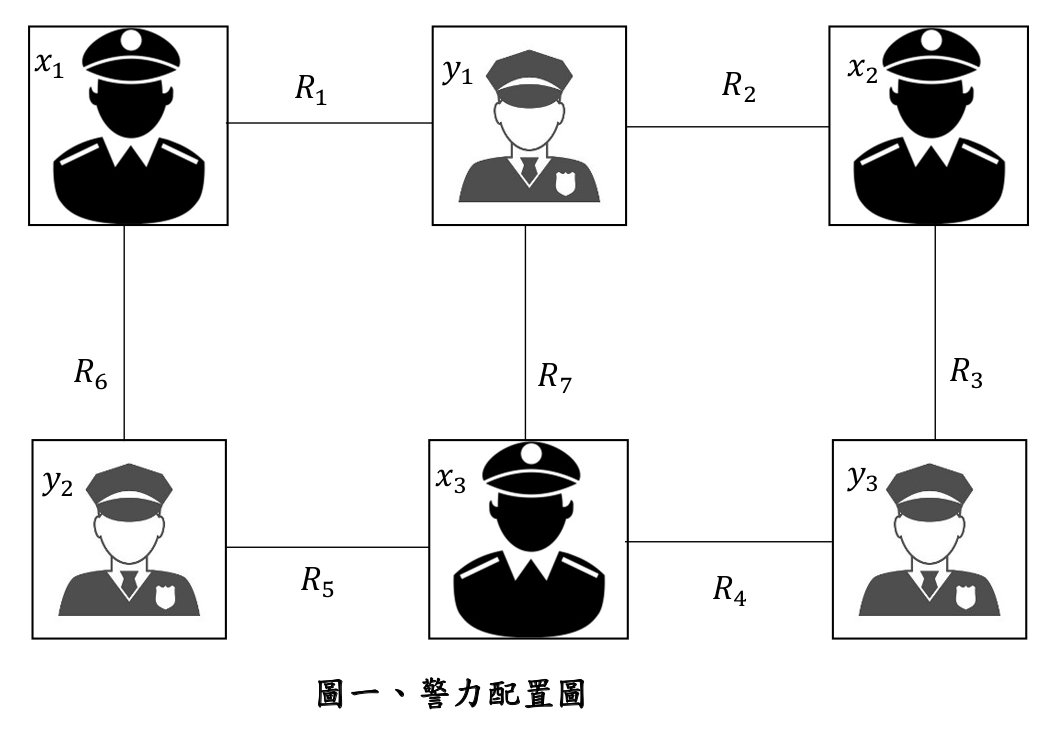
Input Format
第一行有 1 個不大於 10 的數字代表此子題測資的數目。接下來每組測資的第一行有 3 個數字,代表
Output Format
針對所輸入的資料,輸出能滿足任務的最小的組長個數。
Sample Input 1
1 3 4 5 1 2 1 3 2 1 2 3 3 4
Sample Output 1
3
Sample Input 2
1 2 2 3 1 1 2 2 1 2
Sample Output 2
2
Sample Input 3
1 5 4 8 1 1 1 4 2 1 3 2 3 4 4 4 5 1 5 3
Sample Output 3
4
Hints
本題共有五個子題,每一子題可有多筆測試資料:
第一子題的測試資料
第二子題的測試資料警力配置圖為一條路徑(path),
第三子題的測試資料警力配置圖為連結圖(connected)且不存在環路(cycle)。圖形為連結圖代表此圖的任意兩個不同的節點皆存在一條路徑;而環路表示起點和終點為同一節點的路徑。
第四子題的測試資料
第五子題的測試資料
Problem Source
106學年度高級中學資訊學科能力競賽決賽 程式設計試題第四題
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 15 |
| 2 | 1 | 19 |
| 3 | 2 | 27 |
| 4 | 3 | 29 |
| 5 | 4 | 10 |
