1988 . 乘法指令 (Multiply)
TopCoder
Description
在古老的年代,電腦是以一個一個的記憶單元組成的,指令也不多。現在我們要來模擬這種電腦把兩個2位數相乘的計算過程。
我們假設這個電腦使用
在程式執行開始之前,電腦會被植入一或兩個函數
另外,
下圖舉例

這種電腦的指令只有一種:
現在,你要透過設定電腦的函數
同樣以

給定
Input Format
本題輸入只有一行,包含一個正整數
本題有許多子任務。保證存在單一方法可以完成所有子任務。
以下以
| 子任務 (測資) |
額外限制 | 分數 |
| 1 (0) | 10 | |
| 2 (1) | 10 | |
| 3 (2) | 10 | |
| 4 (3) | 5 | |
| 5 (4) | 5 | |
| 6 (5) | 5 | |
| 7 (6) | 5 | |
| 8 (7) | 5 | |
| 9 (8) | 5 | |
| 10 (9) | 5 | |
| 11 (10) | 5 | |
| 12 (11) | 5 | |
| 13 (12) | 5 | |
| 14 (13) | 5 | |
| 15 (14) | 5 | |
| 16 (15) | 5 | |
| 17 (16) | 5 |
Output Format
第一行請輸出一個正整數
接下來
接下來一行輸出一個數字
接下來
如果你輸出的格式不對,或值域不符合題目、子任務之限制,你會獲得一個WA。
Sample Input 1
Sample Output 1
#Sample Output 1
1
0 2 1
1 2 2
2 1 1
4
1 2 7
7 7 7
2 8 8
8 7 5
#Sample Output 2
2
0 2 1
1 2 2
2 1 0
1 2 0
2 1 0
1 1 2
3
1 2 4 0
5 5 5 1
4 2 4 1
Hints
以Sample Output 1為例,假設
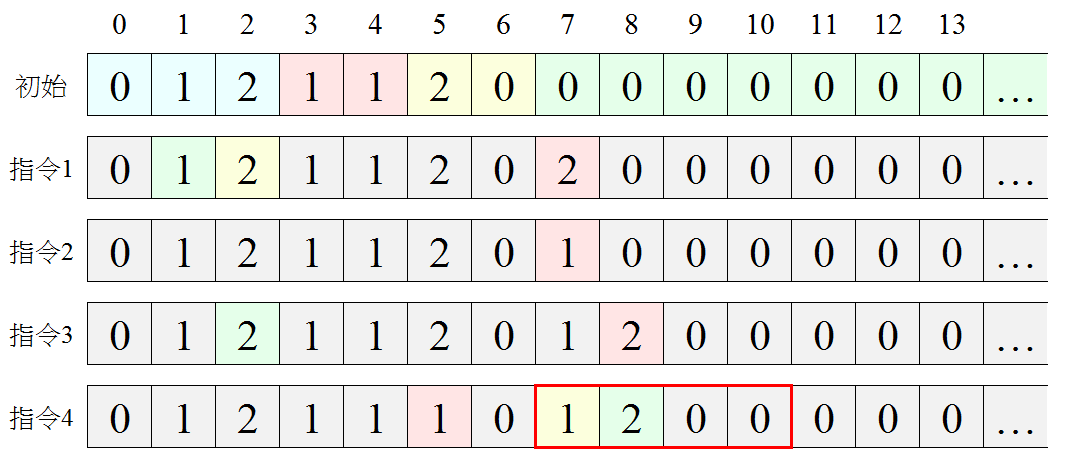
執行結束後儲存答案的記憶單元(編號7~10)的內容是1200(也就是十進位的45),但是由於
Problem Source
改編自CodeChef Challange 2017/07
Problem Set / Judge by Yihda Yol
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 10 |
| 2 | 1 | 10 |
| 3 | 2 | 10 |
| 4 | 3 | 5 |
| 5 | 4 | 5 |
| 6 | 5 | 5 |
| 7 | 6 | 5 |
| 8 | 7 | 5 |
| 9 | 8 | 5 |
| 10 | 9 | 5 |
| 11 | 10 | 5 |
| 12 | 11 | 5 |
| 13 | 12 | 5 |
| 14 | 13 | 5 |
| 15 | 14 | 5 |
| 16 | 15 | 5 |
| 17 | 16 | 5 |
