1719 測資加強 已 rejudge
1939 . 網路建設 (Fibers)
TopCoder
Description
抓寶網路公司正在幫和平社區規劃新一代的網路架構，該社區的網路平面架構圖如下，其中有編號的頂點代表網路設備的位置，兩個相鄰頂點之間有一虛線段連接，線段部分代表可以鋪設網路光纖的路線，網路設備可以透過光纖連結起來。
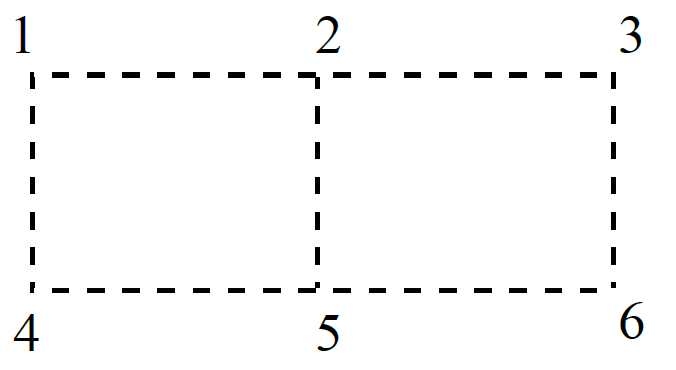
工程師發現只要用5 段光纖就可以將這6 個設備連接起來，下圖為兩種可能的連結方法，事實上還有其他連結的方式。工程師想知道總共會有幾種相異的連結方法，可以用最少的線段把所有的網路設備連結起來。
一般而言可將上述平面架構圖延伸為2N (N ≥ 3)個頂點，上排頂點的編號為1 到N，下一排的頂點編號由N+1 至2N，其中頂點I (1 ≤ I ≤ N)與頂點I+N 相鄰，另外對於頂點I (1 < I < N， N+1 < I < 2N) 分別與頂點I-1 及 I+1 相鄰。請寫一程式，幫工程師計算出總共有幾種相異的連結方法。因答案可能很大，程式輸出的答案為「原始答案」除以$10^ 9+9$的餘數。
Input Format
第一列為一個正整數 T，代表測試資料的個數，T ≤ 10。接下來的 T 列，每一列有一個正整數 N，1 ≤ N ≤ 100。
Output Format
每筆測試資料各有一列輸出，即所有相異連結的總數，因答案可能很大，只要輸出原始答案除以$10^ 9+9$ 的餘數即可。
Sample Input 1
3
1
2
3
1
2
3
Sample Output 1
1
4
15
4
15
Hints
本題共有二個子題，每一子題可有多筆測試資料：
第一子題的測試資料 T ≤ 5，N ≤ 5，全部解出可獲31 分；
第二子題的測試資料 T ≤ 10，N ≤ 100，全部解出可獲69 分。
Problem Source
105學年度高級中學資訊學科能力競賽決賽 程式設計試題第二題
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 31 |
| 2 | 1 | 69 |