1787 . Ch6. Section 2. 醬油
TopCoder
Tags
Description
放學了, 整天都不見妁艷的妤嬌很擔心. “噫! 妁艷好女色.” 妤嬌這時想到妁艷家附近的女校, 妁艷一定是被吸進去了.
“今天的我沒有極限!!!”
只消 10 分鐘, 妤嬌便到達妁艷家附近了. 這時前方路上出現了一位少女. “葛格不見了 所以我跑去添購” , 少女騎著單車說,
“欸? 蒼蠅?”“啊 飛走了” 身為天才的妤嬌看到了少女, 立刻知道了她是妁艷的妹妹. 妤嬌知道, 要觸發接下來的事件, 一定要被少女撞倒然後假裝受傷!
妤嬌看見眼前有 n 條平行且向前延伸的道路, 而少女在這 n 條道路的另一端.
這些平行道路之間, 有些單向或雙向的小路連結兩條相鄰的道路, 這些小路都和 n 條道路垂直.
少女在 n 條道路的一端, 而妤嬌在另一端, 而且少女正在往妤嬌的方向前進.
少女可能在向前的過程中經過小路而更換行進的道路, 但是少女永遠不會向後 (即妤嬌面對的方向)騎.
妤嬌想知道, 若少女從那端的哪些道路開始騎, 會使得妤嬌不論站在自己這端的 哪一條道路, 都有可能被撞.
此外, 別小看妤嬌, 妤嬌是個超能力者, 妤嬌具有“打通小路隧道程度的能力”.
除了原本的 m 條小路之外, 妤嬌還可以自行打通 k 條單向小路在任意地方(事先 打好), 來增加被撞的機會.
妤嬌想讓符合上述條件的道路(從那邊開始騎, 能讓妤嬌不論站在哪都可能被撞) 最多.
你要幫妤嬌安排要打通的小路, 並告訴他最多能有多少道路滿足條件.
Input Format
第一行有四個整數 n, m, p, k
(2≤n≤100,000 , 1≤m,k≤100,000, 0≤p≤100,000) 分別代表平行道路的數量, 每條道路的共同長度, 原本道路之間的小路的數量, 妤嬌能打通幾條小路. 接下來有 p 行代表原本的 p 條小路. 每行有三個整數 ni, mi, di
(1≤ni ≤n-1, 0≤mi ≤m, 0≤di ≤1) 分別代表第 i 條小路是向妁艷妹妹的右手邊(di = 0), 或左手邊(di = 1), 連接左手邊屬來第 ni, ni+1 條道路, 且位在妁艷妹妹前方 mi 個長度單位. 注意兩條小路的位置有可能相同.
Output Format
輸出安排好打通的小路後, 最多能多多少道路滿足條件.
要打通的小路‘不必’在距離妤嬌整數單位長的地方.
Sample Input 1
4 3 5 2 2 0 0 2 2 1 3 3 1 1 1 1 3 3 0
Sample Output 1
2
Hints
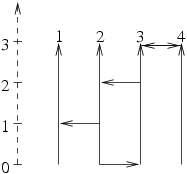
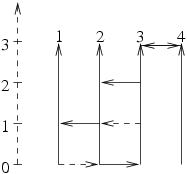

騎車記得帶安全帽
Problem Source
原TIOJ1787 / source: POI XIV Driving Exam
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 10 |
| 2 | 1 | 10 |
| 3 | 2 | 10 |
| 4 | 3 | 10 |
| 5 | 4 | 10 |
| 6 | 5 | 10 |
| 7 | 6 | 10 |
| 8 | 7 | 10 |
| 9 | 8 | 10 |
| 10 | 9 | 10 |
