1740 . [APIO '08] Roads [Interactive]
TopCoder
Tags
Description
新亞洲王國內共有 M 條道路連結 N 個村莊。
有些道路是鵝卵石路,有些則是混凝土路。
要使所有道路能免費供人民使用就需要龐大的支出,目前似乎不太可能的做到,
所以王國需要一個新的道路維護計畫。
國王最終決定要保留越少道路越好,但是每兩個不同的村莊之間一定要有一條,且是唯一的一條免費的路徑相連。
此外,雖然混凝土路比較符合現今道路需求,國王認為走在鵝卵石路上是比較有趣的,因此他決定要剛好保留K條免費的鵝卵石路。
舉例來說,假設新亞洲王國的村莊與道路如圖1(a)所示,如果國王要保留兩條免費的鵝卵石路,
那就可以如圖1(b)將道路 (1, 2), (2, 3), (3, 4) 和 (3, 5) 保留為免費通行。
此安排符合國王的要求因為
(1)每兩個村莊之間都有一條免費道路,
(2)免費道路越少越好,
(3)所有免費道路中剛好有兩條鵝卵石路,即 (2, 3) 和 (3, 4)。
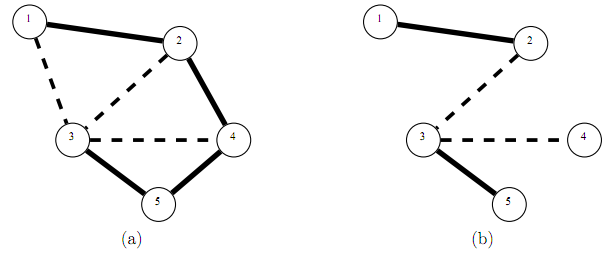
圖1:
(a)新亞洲王國村莊與道路範例。實線代表混凝土路,虛線代表鵝卵石路。
(b)一個含有兩條免費鵝卵石路的道路維護計畫,圖中只畫出免費道路。
給定新亞洲王國的道路圖,與國王所想要保持免費的鵝卵石路數量,
請寫一個程式來判斷是否有可以符合國王要求的道路維護計畫,
如果有,請輸出該計畫。
Input Format
本題為互動題,需要引入標頭檔#include "lib1740.h"。
void Init(int &n, int &m, int &k, int U[], int V[], int C[]);
一開始需要呼叫這個函數。
你會得到N, M, K。
N,代表村莊數 (1 ≤ N ≤ 20,000)
M,代表道路數 (1 ≤ M ≤ 100,000)
K,代表國王要求保留免費的鵝軟石路數量 (0 ≤ K ≤ N - 1)
U, V, C請傳入一個有M個元素的陣列指標,之後這個函式會把值寫進去。
然後第i項的元素,U[i], V[i], C[i], (0 <= i < M)
表示第i+1條的道路其連接村莊U[i], V[i],村莊以數字 1 ~ N 表示之。
C[i]代表這條道路的型態
若 C[i] = 0 則是鵝卵石路;若 C[i] = 1 則是混凝土路。
每兩個村莊之間不會有超過一個連接兩村莊的道路。
void Solution(int u, int v, int c);
void NoSolution();
若是不可能有一個符合國王要求的道路維護計畫,則呼叫一次NoSolution。
否則,你應該呼叫N-1次Solution傳入該維持免費的道路。
傳入的道路格式應與你得到的該道路的描述格式相同u對應U[], v對應V[], c對應C[],
道路的傳入順序不限制,任何順序皆可。
若是有一個以上符合要求的道路維護計畫,則只需要傳入其中一個即可。
提供範例程式和範例標頭檔下載。
使用範例標頭檔,需要給定合法的Input。
合法的Input第一行有三個整數N, M, K,以空白隔開。
接下來的 M 行描述新亞洲王國的道路狀況,第 (i+1) 行代表道路i,每一行都有三個以空白隔開的整數U[i], V[i], C[i]。
Output Format
Sample Input 1
5 7 2 1 3 0 4 5 1 3 2 0 5 3 1 4 3 0 1 2 1 4 2 1
Sample Output 1
Solution(3, 2, 0); Solution(4, 3, 0); Solution(1, 2, 1); Solution(5, 3, 1);
Hints
Problem Source
原TIOJ1740 / APIO '08
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 9 |
| 2 | 1 | 9 |
| 3 | 2 | 9 |
| 4 | 3 | 9 |
| 5 | 4 | 9 |
| 6 | 5 | 9 |
| 7 | 6 | 9 |
| 8 | 7 | 9 |
| 9 | 8 | 9 |
| 10 | 9 | 9 |
| 11 | 10 | 10 |
