1719 測資加強 已 rejudge
1578 . 調和三角（triangle）
TopCoder
Description
「調和三角(Leibniz harmonic triangle)」是數學家Leibniz 所提出的一個數學模型，可以用來解決許多求無窮級數和的問題。
「調和三角」的原理「Pascal 三角」十分相似，如下圖所示，假設「調和三角」中第r 行第c 個元素的值為L(r,c)，
則 L(r,c) = L(r-1,c-1) - L(r,c-1)；同時 L(r,1)=1/r，L(r,r)=1/r，且r≧c≧1。
「調和三角」具有一些有趣的性質，例如
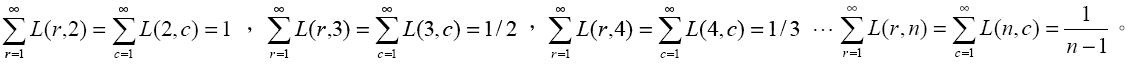
由於「調和三角」的計算十分費時，請你寫一個程式，在給定r 與c 的值後，能夠快速地幫數學家們計算出正確的L(r,c)值。
Input Format
輸入檔中的第一行有兩個以空白相間隔的正整數，分別依次為 r 與 c。為簡化計算過程起見，
我們假設這兩個正整數必介於 1 與 28 之間(包含 1 和 28)，同時 r≧c。
Output Format
請根據輸入檔的資料，輸出L(r,c)的倒數值。
註: 在所有的測試資料中，L(r,c) 的倒數值皆為小於 1,000,000,000 的正整數。
Sample Input 1
5 3
Sample Output 1
30
Sample Input 2
28 12
Sample Output 2
365061060
Hints
Problem Source
原TIOJ1578 / 台北市 97 學年度高級中學資訊學科能力競賽
Subtasks
| No. | Testdata Range | Score |
|---|---|---|
| 1 | 0 | 20 |
| 2 | 1 | 20 |
| 3 | 2 | 20 |
| 4 | 3 | 20 |
| 5 | 4 | 20 |