給定一個由整數所組成的正方形矩陣，其大小為N×N(亦即列、行數均為N)。令W為一矩形的框子，其大小為a×b (其中1<=a<=N，1<=b<=N)，則W 所形成之子矩陣為將W 置於該正方形矩陣內時，W 所框出的小矩陣。由於W 的大小及位置均可變動，因此可在給定的正方形矩陣中形成許多的子矩陣。請寫出一程式能找出一子矩陣，該矩陣中元素的加總值是所有子矩陣中最大的，稱為總和值最大的子矩陣；由於總和值最大的子矩陣可能有許多個，程式只要輸出總和值即可。

例如一個正方形矩陣如下：

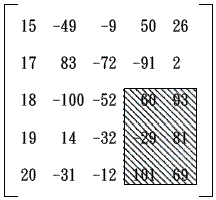
則框線標示出來的就是總和值最大的子矩陣，總和值為60 + 93 + (-29) + 81 + 101 + 69 = 375。

程式計算如下：
　　首先必須依照輸入的兩個數值自動產生方形矩陣。
　　令正方型矩陣中第i列第j行的元素為a_ij(1<=i<=N；1<=j<=N)，則正方形矩陣為
　　
　　其產生方式如下：給予N和a₁₁，矩陣中的元素可根據下列式子自動產生。
　　
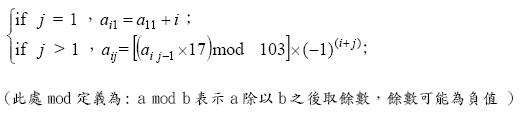
　　再依據上述計算產生出的N×N 陣求出所有子矩陣中最大的總和值作為程式輸出。