1034 . 搶救雷恩大兵 (Saving Ryan)
TopCoder
Tags
Description
米勒上尉收到一道緊急命令，要求將二等兵雷恩即刻護送至指定地點。米勒上尉馬上攤開戰場地圖，希望能規畫出一條最安全的路線。戰場地圖可視為一個 N×N 的表格，表格中的每個位置只可以往東、南、西、北四個鄰近的位置移動。根據情報，米勤上尉已經掌握每個位置的敵軍兵力，所謂最安全的路線，指的是這條路線上所有敵軍兵力總和最小的路線。
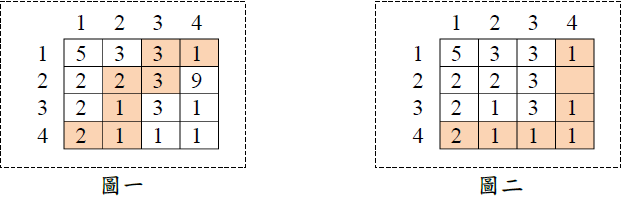
以圖一為例，圖中的數字代表敵軍兵力。如果雷恩目前在 (4, 1) 的位置，需要被護送到 (1, 4) 的位置，則最安全的路線為 (4, 1) → (4, 2) → (3, 2) → (2, 2) → (2, 3) → (1, 3) →(1, 4)，路線上的敵軍兵力總數是 2+1+1+2+3+3+1 = 13。
由於雷恩非常重要，因此上級決定支援米勒上尉。米勒上尉可以用「一發」死光炸彈轟炸地圖上的「一個」位置，轟炸過後該位置的敵軍將灰飛湮滅。以圖二為例，如果米勒
上尉轟炸了 (2, 4) 位置，則新的最安全路線將變成 (4, 1) → (4, 2) → (4, 3) → (4, 4) → (3,4) → (2, 4) → (1, 4)，路線上的敵軍兵力總數是 2+1+1+1+1+0+1 = 7。
請撰寫一個程式，幫助米勒上尉找出在一發死光炸彈支援下，最安全路線的敵軍兵力總數。
Input Format
輸入的第一行有一個正整數 $N (1 \leq N \leq 20)$，代表地圖大小為 $N \times N$。
接下去有 $N$ 行，第 $i$ 行有 $N$ 個正整數 $e_{ij}$ $ (1 \leq e_{ij} \leq1000, 1 \leq i, j \leq N)$，代表地圖中每個位置 $(i, j)$ 的敵軍兵力數。數值之間以至少一個空白隔開。
下一行有一個正整數 $Q (1 \leq Q \leq N^ 4)$，代表可能的詢問數。
再接下去有 $Q$ 行，每行有四個正整數 $x_{q0}, y_{q0}, x_{q1}, y_{q1} $ $(1 \leq x_{q0}, y_{q0}, x_{q1}, y_{q1} \leq N, 1 \leq q \leq Q)$。$(x_{q0}, y_{q0}) $為雷恩的出發位置，$(x_{q1}, y_{q1})$ 為雷恩的目的位置。數值之間以一個空白隔開。
Output Format
請輸出 $Q$ 筆答案，每個答案$a_q$ 一行，代表一發死光炸彈支援下，從 $(x_{q0}, y_{q0}) $到$(x_{q1}, y_{q1})$ 最安全路線的敵軍兵力總數。
Sample Input 1
1 10 2
1 1 100
1 100 1
2
1 1 1 2
2 1 3 3
Sample Output 1
3
Sample Input 2
5 3 3 1
2 2 3 9
2 1 3 1
2 1 1 1
3
4 1 1 4
4 4 2 3
3 1 2 4
Sample Output 2
5
7
Hints
Problem Source
臺北市104 學年度高級中學資訊學科能力競賽程式設計試題第五題
Set by Paupière
若測資有誤請儘快聯絡管管(?
Subtasks
| No. | Testdata Range | Constraints | Score |
|---|---|---|---|
| 1 | 0~4 | $e_{ij} = 1$ | 10 |
| 2 | 5~9 | 若 $i \neq j$ 則 $e_{ij} = 1$，其餘 $i = j$ 且 $e_{ij} = 1000$ | 10 |
| 3 | 10~14 | 所有詢問的目的位置均相同 $(x_{11} = x_{21} = x_{31} = … = x_{Q1}, y_{11} = y_{21} = y_{31}= … = y_{Q1})$ | 40 |
| 4 | 15~19 | 沒有特別的條件限制 | 40 |